들어가기
라인 오프셋은 라인에서 일정한 간격으로 떨어져서 그려진다. 단순한 라인이라면 쉽지만 폴라라인인 경우 라인이 만나는 부분에서 쉽지가 않았다. 그러나 해결책을 알고는 너무 쉬워졌다. 어떻게 처리 했는지 알아보자.
작성자: http://ospace.tistory.com/ (ospace114@empal.com)
라인 오프셋 단순한 접근
먼저 폴라라인으로 시작하면 복잡하니 라인부터 시작해보자. 예를 하나 보자.
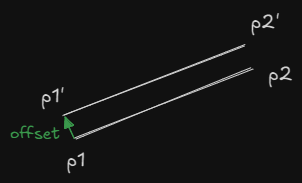
점 p1과 p2로된 직선이 있고 직선의 수직 방향으로 offset 크기만 큼 떨어져서 점 p1’과 p2’로된 직선이 그려진다. 이 작업은 생각보다 어렵지 않아보인다.
처음 접근한 방법을 직선의 각도를 알면 오프셋의 각도를 알 수 있고 이를 사용해 오프셋한 위치의 점을 계산할 수 있다고 판단했다.

점 p1과 p2의 직선의 각도가 θ가 된다. 그리고 점 p1의 오프셋된 위치인 점 p1’에 y축 기준으로 각도 θ가 된다. 점 p1의 좌표가 (x1, y1)인 경우 점 p1’의 좌표를 구해보자.
$$ x = x1+\sin \theta \times offset\\ y = y1+\cos \theta \times offset $$
그다지 어렵지 않게 구할 수 있었다. 이제 폴리라인에 대해서 적용해보자.
폴리라인에서 오프셋
폴리라인에서 오프셋도 앞의 라인 오프셋처럼 단순해보일 수 있다. 일정 오프셋 거리만큼 떨어지면 되기에 큼 어려움이 없어 보인다. 아래 폴리라인 예를 보자.

점 p1의 오프셋은 점 p1’이 된다. 점 p2의 오프셋은 점 p2-1’이 된다. 다시 점 p2와 점 p3인 직선 기준으로 점 p2의 오프셋은 점 p2-2’이 된다. 여기서 이상해진다. 점 p2의 이상적인 오프셋 위치는 점 p2’이 되어야하지만 이를 이전 방식처럼 단순하게 구할 방법이 없다. 두 직선이 직각으로 만나지 않는 경우도 있기에 복잡한 연산이 필요하게 된다.

먼저 이전 라인 오프셋처럼 오프셋 각도 θ1을 사용해 점 p2의 오프셋인 점 p2-1’위치를 구한다. 그리고 다시 점 p2와 점 p3의 라인에 대한 수직 방향인 점 p2-2’으로 오프셋을 보자. 이때에 오프셋 각도 θ2를 구할 수 있다. 이 각도를 활용해 점 p1과 점 p2 직선 상에 투영되는 길이를 구할 수 있다. 이 길이가 점 p2-1’과 점 p2’ 직선이 길이가 된다. 다시 이 길이와 오프셋 각도 θ1을 사용해 점 p2’의 좌표를 구할 수 있다.
추후 점 p2에서 점 p2-2’으로 오프셋 작업할 때 연산을 줄이기 위해서 이전 연산을 재사용할 수 있는 방안으로 조금이나마 성능을 올릴 수 있다. 이 방식으로 연산하지 않기에 별도 수식은 작성하지 않았다. 이제 개선안을 살펴보자.
폴리라인에서 오프셋 개선안
이전 방식으로는 너무 많은 연산과 복잡한 수식이 필요하다. 이를 개선할 수 있는 방법이 벡터를 사용하는 방법이다. 벡터 중에 직교벡터를 사용하면 된다. 점 p1의 좌표(x1, y1)과 점 p2의 좌표(x2, y2)로 된 벡터가 있을 경우 직교 벡터(x,y)를 구해보자. 직교벡터는 단위벡터로 구한다.
$$ dx = x2-x1\ dy = y2 - y1\\ length = \sqrt {dx \times dx + dy \times dy}\\ (x,y) = \left (-\frac {dy}{length}, \frac {dx}{length} \right) $$
직교 벡터를 구하면 이후 부터는 연산이 단순해진다. 앞의 예를 가지고 살펴보자.

$\hat o 1$은 점 p1과 점 p2 직선에 대한 직교벡터이고 $\hat o 2$는 점 p2과 점 3 직선의 직교벡터이다. 점 p1의 오프셋은 점 p1’을 구하는 작업이 쉽다.
$$ p1' = p1 + \hat o 1 \times offset $$
문제의 점 p2’을 구하는 방법을 보자. 점 p2에서 보면 양쪽 직교 벡터가 만나서 합쳐지는 부분이다. 이때 합쳐지는 직교벡터 $\hat o 3$를 구하면 된다. 이는 단순히 벡터 합을 하면 된다.
$$ \hat o 3 = \hat o 1 + \hat o 2 $$
이제 점 p2’를 구해보자.
$$ p2' = p2 + \hat o 3 \times offset $$
점 p3’도 이전 방식으로 구할 수 있다. 모든 점이 구해졌으니 선만 그리면 된다.
마무리
별거 아닌 폴리라인 오프셋이 생각보다 어려웠다. 그런데 알고보지 그렇게 어렵지는 않다. 삼각함수로 복잡한 연산이 벡터를 활용해서 간단히 끝낼 수 있었다. 의외로 벡터가 그래픽 처리할 때에 자주 사용된다. 어떻게 보면 컴퓨터 연산에 더 효율적이기 때문에 더 활용된다고 볼 수 있다. 아마도 이글을 보는 여러분은 벡터 공부를 하고 싶어질 것이다.
부족한 글이지만 여러분에게 참고가 되었으면 하네요. 모두 즐거운 코딩생활하세요. ospace.
참고
[1] 나무위키, 벡터, https://namu.wiki/w/%EB%B2%A1%ED%84%B0, 2025.04.04
[2] ospace, 수학기초 4- 벡터, https://ospace.tistory.com/999, 2025.02.18
'6.수학과 알고리즘' 카테고리의 다른 글
| 수학기초 9 - 정보이론 (0) | 2025.05.02 |
|---|---|
| [알고리즘] 행렬 회전 (2) | 2025.04.11 |
| [그래픽] 폴리라인에서 곡선처리 (1) | 2025.04.02 |
| 수학기초 8 - 확률과 통계 2 (0) | 2025.03.27 |
| 수학기초 7 - 확률과 통계 1 (0) | 2025.03.19 |


